Chapter 5 – Coastal Sediment Processes
- Chapter 1 – Introduction
- Chapter 2 – Coastal Highways
- Chapter 3 – Tides, Storm Surge and Water Levels
- Chapter 4 – Waves
- Chapter 5 – Coastal Sediment Processes
- Chapter 6 – Coastal Revetments for Wave Attack
- Chapter 7 – Roads in Areas of Receding Shorelines
- Chapter 8 – Highway Overwashing
- Chapter 9 – Coastal Bridges
From ‘Highways in the Coastal Environment: Second Edition’ by FHWA
Chapter 5 – Coastal Sediment Processes
5.1 – 5.2 – 5.3 – 5.4 – 5.5 – 5.6 – 5.7
The coastline is a unique geological environment. Sediments along the coast are constantly being reshaped by waves and other currents. These processes, primarily sand movement, can have significant implications for engineers tasked with working in this environment. The study of coastal sediment processes includes several specialty areas of coastal geology including coastal geomorphology, the study of coastal landforms and features, and coastal sedimentology, the study of the properties of beach sands. A good understanding of the terminology and concepts of coastal geology is valuable for coastal engineering.
The design function of many coastal engineering projects is to positively affect coastal sediment processes. Two of the primary functions of coastal engineering projects, beach erosion control and navigation improvement, are often contradictory, however. Many coastal engineering projects which have improved navigation, such as inlet or harbor jetties and dredging, have caused nearby beach erosion. An improved understanding the coastal processes and the geological framework at work at each location can lead to better designed coastal engineering projects.
This Chapter provides a brief introduction to some coastal sediment processes including an overview of coastal geology, beach terminology, coastal sediment characteristics and transport, and tidal inlets. Just a few of the other textbooks and references with much more detail on these topics include Komar (1998), Dean & Dalrymple (2002), Kamphuis (2000), Davis & Fitzgerald (2004), Davis (1994), and the CEM (USACE 2002) and the SPM (USACE 1984).
5.1 Overview of Coastal Geomorphology
America’s coast has many different characteristics. Coastlines in the United States include the extensive barrier islands systems of the south Atlantic and Gulf coast as well as the coastal bluffs of New England, the Pacific, and the Great Lakes. A few coasts are muddy shorelines (the “big bend” of Florida) or vegetated shorelines (mangroves of southwestern Florida) but these are the exceptions. Some coasts are rock cliffs that extend into the sea and are pounded by relentless ocean waves. But, most of America’s coasts have some form of sandy shoreline.
Beaches, the accumulations of loose sediments along the shoreline can either be barrier islands or just short pocket beaches between two rock headlands. The type of coast and beach at each location is partially controlled by the “geologic framework” that created it. This framework includes the local geologic formations and the interplay between plate tectonics, sea-level changes and waves that have created each beach.
Coastal geomorphology is the study of coastal landforms. Many of the most obvious coastal landforms are products of either erosional processes or depositional processes. Sea cliffs, stacks, arches, caves and wave cut terraces are some erosional features found on retreating rocky coasts (see Figure 5.1). Figure 5.2 shows a sea cliff on the Pacific coast. Note that there is a small beach at the base of the cliff. This is a pocket beach that forms from sand eroded out of the cliff and off the immediate uplands and is held in place by the headlands where the cliffs extend to the sea at the ends of the beach.
Barrier Islands, spits, bays and lagoons are some depositional features found on along much of the United States sandy coasts (Figure 5.3). Figure 5.4 shows the barrier island chain of the Outer Banks of North Carolina.
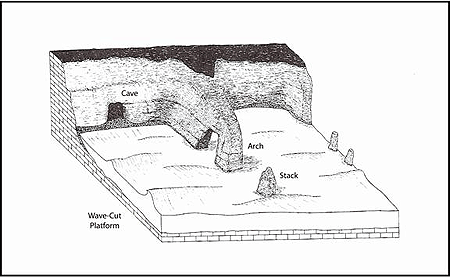
Figure 5.1. Erosional features associated with rocky coasts (from Komar 1998)

Figure 5.2. Sea cliff in San Diego California with pocket beach

Figure 5.3. Features associated with depositional coasts (from Komar 1998)

Figure 5.4. Barrier islands of the Outer Banks of North Carolina
One of the fundamental geologic controls on shoreline position and characteristics is sea level. Sea level has fluctuated tremendously throughout the past two million years. Chapter 3 discusses the sea level change experienced along the United States shorelines during the past century. However, the history of sea level changes over the past 2 million years, and particularly the past 20,000 years has had an impact on the coastlines we have today. During the ice ages, worldwide sea level fell as glaciations increased and rose as the glaciers receded.
The worldwide, eustatic (with land elevation changes removed), sea level was probably 100 m lower 20,000 years ago than it is today according to geologist’s estimates. One estimate of the rate of sea level rise in the past 20,000 years is shown in Figure 5.5. This time period, particularly the past 12,000 to 20,000 years, is the Holocene Epoch at the end of the Quaternary Era. It is characterized by the rise of global sea level in response to the melting of the last of the Wisconsin ice-age glaciers (Davis and Fitzgerald 2004).

Figure 5.5. Sea level change curves for the past 20,000 years (adapted from Davis 2004)
The Holocene rise in sea level (Figure 5.5) has two distinct portions. Prior to about 5,000 to 7,000 years ago, sea level rose at a much faster rate. The rate of sea level rise was about 10 mm/year or 1 m/century. When the sea level was rising at such a fast rate, it is possible that the coastline moved very inland and mature barrier islands did not have the time to form. The rate of rise slowed significantly about 5,000 years ago. This allowed the shorelines to become more stable and wave-driven longshore sand movement to create the barrier island systems along many of our shores today.
The question marks shown on Figure 5.5 represent the uncertainty about the way that the Holocene rise in sea level occurred. Some investigators postulate that there was significant fluctuation and others do not. Most, however, agree with the general shape of the curve shown.
The position and characteristics of shorelines are partially controlled by global plate tectonics (Inman and Nordstrom 1971). The Pacific coast of the United States is on the “leading” edge of the North American plate and the Atlantic coast is on the “trailing” edge of the plate. The difference explains some of the general differences in shoreline characteristics including the presence of mountain ranges and a narrow continental shelf near the Pacific Coast but not the Atlantic coast (Davis 1994). These are contributing factors to the lack of barrier island systems on the Pacific Coast and their extensive presence on the Atlantic coast.
5.2 Beach Terminology
The beach can be defined as the accumulation of unconsolidated sediment (sand, gravel, and/or cobbles) extending from some upland location, such as a sea cliff or sand dune or vegetation line, to the water line and extending out below the water to a depth where the sediment is not moved by wave action. The beach is commonly synonymous with the term “littoral” referring to this same area where waves can move sand (Komar 1998). The offshore limit of the littoral zone can be very deep during large storms but is often just assumed to be a depth of 20 to 60 feet depending on the wave climate.
Terminology used to describe the processes of waves and currents in the nearshore is shown in Figure 5.6. The nearshore zone extends from the upper limit of wave runup on the beach to just beyond where the waves are breaking. The breaker zone or line is the portion of the nearshore region in which waves arriving from offshore become unstable and break (see Chapter 4). The swash zone is the portion where the beach face is alternately covered by the run-up of the wave swash and then exposed by the backwash. The surf zone is the portion of the nearshore between the breaker line and swash zone. The surf zone can have bore-like, breaking or broken waves propagating across it. The field of “surf zone dynamics” is an active area of research that focuses on the hydrodynamic motions of waves and currents as well as the sediment response to those motions in the surf zone.

Figure 5.6. Terminology used to describe processes of waves and currents in the surf zone (Komar 1998)
The shape of a beach profile, or transect or cross-section, has some typical features. The terminology used to describe the beach profile is shown in Figure 5.7. A longshore bar, or sand bar, is an underwater ridge of sand running roughly parallel to the shore. Sand bars can be exposed at low tide in areas with large tide ranges. Figure 5.8 shows a sand bar exposed at low tide at a location along the South Carolina coast that has a tide range of about 7 feet. Because of the beach slope, the intertidal area here is several hundred feet wide. A longshore trough is a depression inside of a sand bar. The beach face is the area of the swash zone. The beach berm is the nearly horizontal portion of the beach formed by the deposition of sediments by waves. Some beaches have more than one berm at slightly different levels separated by a scarp. A scarp is a nearly vertical cut into the berm portion of the beach profile by wave erosion. Scarps are usually found at the top of the beach face when erosion is occurring. A scarp along a southern California beach is shown in Figure 5.9. Waves were actively eroding the berm at the time the photograph was taken.
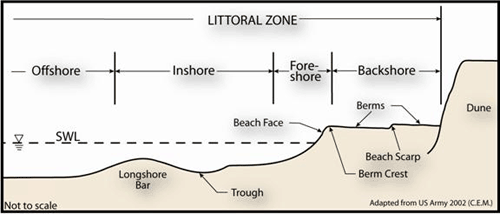
Figure 5.7. Terminology used to describe the beach profile

Figure 5.8. Sand bar and trough exposed at low tide

Figure 5.9. A beach scarp
Repetitive measurements of beach profiles are a common tool in quantifying erosion and other coastal processes. Elevation of the top of the profile’s sand surface, both above the waterline and below the water, is measured. There are a variety of techniques that have evolved over the years for obtaining these measurements. The problem is that neither traditional land surveying techniques nor traditional marine surveying techniques can easily span the offshore, the surf zone, and the upland portions of the beach profile.
Figure 5.10 shows a beach surveying crew using a traditional land surveyor’s level to measure the profile. The rod-man has to wade and swim in the surf zone and this can become problematic in large surf. Distance offshore can be measured with a “tag-line” (see yellow line on beach in Figure 5.10) or an optical or eye-safe-laser rangefinder. One highly specialized modification of this approach is shown in the left side of the photograph in Figure 5.11 where a staff gauge or total reflector station is attached to a CRAB (Coastal Research Amphibious Buggy) that drives out through the surf zone while measurements are made. The CRAB shown in Figure 5.11 is privately owned and used exclusively for measuring beach profiles in beach nourishment projects.

Figure 5.10. Beach profile surveying crew using a traditional level-rod and tag line system

Figure 5.11. A CRAB (Coastal Research Amphibious Buggy) used to measure beach profiles during beach nourishment
Marine surveying techniques have been adapted for the surf zone by placing fathometers and GPS or total stations on jet-skis (personal watercraft). This can improve the ability of the vessel to obtain data in very shallow water.
A relatively recent advance in measuring beach elevations is airborne LIDAR, laser-based elevation measurements, from a helicopter or airplane. One LIDAR system that has been used to make topographic measurements of beach elevation is a joint system of the NASA/USGS/NOAA (see their web-site //coastal.er.usgs.gov/lidar/).
LIDAR technology has the capability of measuring the dry beach elevation and the underwater portion of the profile at the same time with the same equipment. A LIDAR system that measures water depth is the SHOALS system of the Joint Airborne LIDAR Bathymetry Technical Center of Expertise (JALBTCX) which is a joint effort of the USACE, the US Navy, and NOAA (see their web-site //shoals.sam.usace.army.mil/). The water depth measuring LIDAR has some operational limitations related to water clarity and surf zone breaking. The laser can only penetrate water if it is clear enough and the air bubbles in white-capping in the surf zone can cause problems. However, the ability of LIDAR to collect large amounts of precise measurements over large distances in short periods of time is a significant advance for beach profile surveying.
Many beach profiles have similar shapes. If the sand bar is ignored, many beach profiles are concave upward with slopes that are much milder than the angle of repose of the same sands on dry land. This shape is a response to the wave energy present in the surf zone. A useful concept is that of an “equilibrium beach profile” where the shape of the profile is in equilibrium with the wave energy. The shape of the offshore portion of the profile has been modeled with a variety of different expressions. One is shown in Figure 5.12. This simple relationship between depth and distance offshore fits many sandy beach profiles at different locations and has some physical meaning related to the dissipation of energy in the surf zone (Dean 1974, Dean and Dalrymple 2002). The addition of more parameters, including the use of a variable exponent in place of 2/3, can improve the fit of the relationship to any particular profile or set of profiles. The value of the “A” parameter has been shown to be a function of the sand grain size (typically between 0.1<A<0.2).
5.3 Coastal Sediment Characteristics
The sediments on most American beaches are whatever hard, loose sediments are available, based on the local geology. The majority of coastal sediments are sands. Exceptions include the many cobble beaches of the Pacific, New England, and the Great Lakes. Cobbles are round stones and shingles are flatter stones.
Most sand-size sediments on American beaches are quartz or some other hard mineral. Exceptions to this general rule are the many beaches consisting of shell hash, ground up coral reefs, or other carbonate materials that exist in Florida, Hawaii, and to a lesser extent, along many other beaches. The mineral composition of the sand grains depends on the local geologic framework. Figure 5.13 shows the variation in color of beach sands throughout the nation.

Figure 5.12. Dean’s equilibrium beach profile shape definition sketch
The size of the sand grains influences the way a beach behaves and can be important in beach nourishment engineering. Beach sand grain size can vary significantly. Beach sediment grain size can be evaluated with a sieve analysis much like grain size in other civil geotechnical engineering analyses. The median diameter (D50) is the most common measure of sand grain size. Typical median grain sizes for American beaches are 0.15 to 0.60 mm.
The results of a grain size analysis on beach sand are shown in Figure 5.14. The median diameter is about D50 = 0.25 mm. Figure 5.14 shows an important characteristic of beach sand grain size distribution – they can be extremely well-sorted. Essentially, waves can winnow all the other grain sizes away. Since almost all the grains are of the same size, care should be taken to include the full complement of available sieve sizes in order to adequately differentiate beach sand grain sizes with sieve analysis.

Figure 5.13. Examples of colors of US beach sands (from Douglass 2002)
5.4 Cross-Shore Sand Transport and Dune Erosion Modeling
Waves have the capacity to move tremendous amounts of sand in the surf zone. This sand movement on beaches can be conveniently considered as either longshore or cross-shore sand transport. This distinction, cross-shore vs. longshore transport, is somewhat artificial, in that the individual grains of sand may be moved both in the cross-shore and longshore directions at the same time. The movement of individual sand grains in response to wave motion and currents in the surf zone is extremely complex. Movement is related to instantaneous near-bottom water velocities under breaking irregular waves, the resulting shear stress on the bottom sand grains, and the subsequent transport of sand including the rich variations in transport mechanisms (bedload, suspended load, ripple and other bedform effects, bed ventilation effects). The complexities of surf zone dynamics and sediment transport processes preclude any meaningful analytic approaches. Thus, coastal engineers and scientists typically look for simplifications of the dynamics of the processes that can be modeled and compared with empirical results. One of the simplifications adopted is the separation of transport into the cross-shore and longshore directions.

Figure 5.14. Example grain size distribution based on a sieve analysis for beach sand
Coastal practitioners have long understood that sand moves back and forth across a beach profile in response to changes in incident wave energy. This is shown schematically in Figure 5.15.
Wave steepness, the ratio of wave height to wave length, H/L, has a significant impact on whether sand bars are moving onshore or offshore. When the wave steepness is low, such as with swell, sand bars typically migrate to the shore. The sand bars sometimes can move all the way into the dry beach and build up the berm making the dry portion of the beach wider. These low steepness wave conditions typically occur in the summer on the United States Atlantic and Pacific coasts and thus this profile shape, with a wide beach berm, is called a “summer profile.” When waves are steep, such as with a locally generated short period wind sea, sand is eroded out of the berm and the sand bars form or are pulled farther offshore. These sea wave conditions typically occur in the winter and thus, this profile shape is called a “winter profile.” The beach is narrower than for the summer profile. Essentially, the beach profile shape is just moving toward a new equilibrium with the incoming waves. Since incoming waves are always changing steepness through time, the beach may never really reach an equilibrium shape but just always be approaching one.
These seasonal shifts of sand on the beach profile, while they cause a narrowing of the dry, visible beach are not typically the cause of real beach erosion and long-term shoreline changes. However, shoreline recession along a coast which is eroding because of a longshore deficit of sand will appear most obviously after storms. Also, in very large storms, sand can be moved out into sand bar formations and take several years to return to the nearshore system.

Figure 5.15. Typical beach profile changes in response to cross-shore transport of sand
When storm surge temporarily raises the still water level; sand in the berm and dune can be moved out to sea into sand bars. This storm-induced dune erosion can destroy large dune fields in a single major storm. There are several available models for storm-induced dune erosion.
Kriebel (1994) developed a computer-based model, EDUNE, which simulates storm-induced dune erosion by repetitively applying a form of Dean’s energy dissipation concept for equilibrium beach profile shapes. As storm surge rises, the waves begin to attack the berm and dune face and move the sand out into the offshore profile. EDUNE simulates this cross-shore sand movement as the beach profile shape begins to move toward a new equilibrium with the higher water levels.
Inputs into EDUNE are the time histories of the storm surge hydrograph and incident wave heights. There is an empirical coefficient, A, that is the same as that for Dean’s equilibrium beach profile shape and can be related to grain size, but is often used as a calibration coefficient.
Figure 5.16 shows some results of an EDUNE simulation with actual measured dune face erosion. EDUNE has been found to give reasonable results for a variety of major storms and forms of it have been adopted by Florida and Alabama in the management of those state’s coastal construction lines. Unfortunately, EDUNE has not been modernized to run on a Windows-based platform but it still can be used as a compiled FORTRAN program.

Figure 5.16. Kriebel’s dune erosion model results example
The FEMA has adopted a simpler model for storm-induced dune erosion for the purposes of mapping coastal flood plains. FEMA’s model is based on an empirical relationship that relates the volume of sand eroded from the dune directly to the storm return period (Hallermeier & Rhodes 1988):
![]() (5.1)
(5.1)
where:
| (Vol) | = | volume of erosion from the sand dune above the storm surge elevation per unit length of shoreline |
| T | = | return period of storm in years |
| C | = | empirical coefficient: c = 86 when (Vol) is in ft2; c = 8 when (Vol) is in m2 |
Equation 5.1 estimates the volume of erosion for the 100-year and 5-year storm levels as 20 yd3 and 6 yd3 of sand per foot of shoreline, respectively. These values are for the volume of sand above the storm surge elevation (which can be much higher for the 100-year storm). This dune erosion model has been incorporated into FEMA’s Coastal Hazard Analysis Model (CHAMP) model that is available on-line (FEMA 2002).
SBEACH is a computer-based model of cross-shore sand transport developed by the USACE (Larson and Kraus 1989). The model considers four or five different morphodynamic regions (e.g. sand bar, swash zone, dune face) across the surf zone and beach profile and uses empirical models to estimate the beach response in each region while preserving the total amount of sand on the profile. SBEACH can be used for a variety of analyses including cross-shore transport and offshore sand bar movement under the water during non-storm conditions. There are a number of calibration coefficients that can be adjusted to fit actual profile response data. SBEACH can also be used to estimate storm-induced dune erosion but it has been found to be difficult to calibrate to very large storms (it can underestimate erosion). SBEACH is available as a part of the coastal engineering software package Coastal Engineering Design and Analysis System (CEDAS) that is commercially available.
5.5 Longshore Sand Transport and Shoreline Change Modeling
As wave energy enters the surf zone, some of the energy is transformed into nearshore currents and expended in sand movement. The nearshore current field is driven by the incident wave energy and the local winds. The largest currents, in terms of absolute magnitude, are the oscillatory currents associated with the waves. However, several forms of mean currents; including the longshore current, rip currents associated with nearshore circulation cells, and downwelling or upwelling associated with winds; can be important to sand transport.
Longshore current is the mean current along the shore between the breaker line and the beach that is driven by an oblique angle of wave approach (see Figure 5.17). The waves provide the power for the mean current and also provide the wave-by-wave agitation to suspend sand in the longshore current. The resulting movement of sand down the beach is littoral drift or longshore sand transport. This process has been likened to a “river of sand” that flows along all our sandy shorelines. The amount or rate of longshore sand transport can be tremendous during large storms. When averaged over a year, it can exceed a million cubic yards per year moving down the beach some along parts of the American coast. Longshore sand transport, unlike rivers, reverses direction frequently in response to changes in the direction of wave approach. Thus, the net longshore transport rate is significantly less than the gross rate.

Figure 5.17. Definition sketch of wave angle at breaking
If longshore sand transport is interrupted by a ship channel or other engineering works like a jetty system to stabilize an inlet for shipping, erosion can occur for many miles downdrift. The total amount of sand that has been removed, or permanently trapped elsewhere, from America’s beach system by engineering works has been estimated at over 1,000,000,000 yd3 (Douglass, et al. 2003).
The most common equation for estimating longshore sand transport rate is the so-called “CERC Equation” or energy-flux method (USACE 2002). It estimates the sand transport rate based on the longshore component of energy flux or wave power entering the surf zone. Using the expressions for wave power from Chapter 4, the wave-energy flux factor (as evaluated at breaking) can be derived as:
![]() (5.2)
(5.2)
where:
| Pls | = | wave energy flux factor |
| Hb | = | wave height at breaking |
| Cgb | = | wave celerity at breaking |
| = | angle of the breaking wave crest with the shoreline | |
| = | specific weight of water |
The CERC Equation relating this to longshore sand transport can be written as:
![]() (5.3)
(5.3)
where:
| Q | = | longshore sand transport |
| K | = | Empirical coefficient (K=7500 when Q is expressed in yd3/year and Pls in lb/s) |
The relationship between transport rate and energy flux factor is not a precise relationship as shown in Figure 5.18 with field data. Also, there is often uncertainty in estimating the input wave parameters, such as Hb in the CERC equation. In many situations, the CERC equation can be considered as a good order of magnitude estimate of transport.
Shoreline change models simulate the temporal change in shoreline position, i.e. the movement of the shoreline. The CERC equation, or some derivative of it, is used to estimate the longshore sand transport rate at all locations along the shoreline and then conservation of sand down the coast is modeled. The equations are solved repetitively in time for a discretized shoreline. Wave refraction and diffraction have been incorporated into most shoreline change models. The results of shoreline change models are estimates of the changes in shoreline position due to the construction of engineering works such as groins or beach nourishments. Several shoreline change models that are available are Perlin and Dean (1983), GENESIS (Hanson and Kraus 1989), and ONELINE (Dabees and Kamphuis 1998).
Since shoreline change models are essentially multiple applications of the CERC equation or some other longshore sand transport model their results include all the uncertainties inherent in such modeling. Thus, shoreline change models must be adequately calibrated and verified.

Figure 5.18. The CERC equation model for longshore sand transport rate plotted with field data (adapted from USACE 1984)
5.6 Tidal Inlets
Barrier islands are breached by tidal inlets that allow the ocean water to flow into and out of estuarine bays. Two tidal inlets are shown in Figure 5.19. There are hundreds of tidal inlets of various sizes in the US. Oregon Inlet, North Carolina, is an example of a large, unstabilized inlet. Tidal inlets are dynamic parts of the barrier island system that have important influences on the bays and the nearby beaches.
While every inlet is unique, there are some common geomorphological features as shown in Figure 5.20. The flood tide is the movement of water into the inlet and the ebb-tide is the flow of water out of the bay back to the ocean. Typical patterns of the strongest ebb-tide and flood-tide flows are shown by the flow arrows in Figure 5.20. The shoal, or bulge of sand, formed just seaward of an inlet is called the ebb-tidal delta or ebb-tidal shoal. Likewise, a shoal just inside of an inlet is called the flood-tidal delta or shoal. The outer bar of the ebb-tidal delta permits longshore sand transport to naturally bypass an inlet to the downdrift beaches. There are often other shoals inside the outer bar of the ebb-tidal shoal.
The gorge or throat section of the inlet is the main flow channel. It is typically the deepest part of the inlet and has the highest, most concentrated ebb- and flood-tidal flows.

Figure 5.19. Two tidal inlets on the southwest Florida coast (New Pass and Big Sarasota Pass). Lido Key is the barrier island between the two inlets. Net longshore sand transport is to the south.
Tidal inlets are essentially in some dynamic equilibrium between the longshore sand transport system of the adjacent barrier island system and the tidal currents (Bruun 1966). The wave-driven longshore sand transport would seal off the inlet if not for the tidal currents scouring the sand out of the throat and depositing it on the inlet shoals. Most inlets are not symmetrical about their throat like that shown schematically in Figure 5.20 but rather skewed in the direction of net longshore sand transport (e.g. Figure 5.19).

Figure 5.20. Typical inlet morphology
The hydraulics of tidal flows through inlets can be extremely complex due to the shoals, waves and currents. The primary tidal flows can be idealized as shown in Figure 5.21. Water flows into the inlet when the tide in the ocean has risen to a level that exceeds the elevation of the water surface in the bay. This vertical difference in elevation, the head difference, between the ocean and the bay drives the flow much as the downslope gradient in river elevation drives the flow in rivers. The flow in the inlet will continue to “flood” until the tide level in the ocean falls to an elevation below that in the bay. Thus, the bay tide always “lags” the ocean tide. The tidal lag can vary significantly depending on the shape of the bay and inlet.
The amplitude, or range, of the tide in the bay can also be much smaller than in the ocean. This results in an attenuation of the tide range. This is common when the inlet is constricted to a level that does not allow enough time for the bay to completely fill up during the rising ocean tide before the ocean tide begins to fall. In many cases, the tide range can actually increase farther up an estuary due to inertial effects. There are a number of quasi-analytical models of the solutions to the idealized ocean-inlet-bay system including solutions for maximum velocity in the inlet and bay tidal range amplitude (USACE 1984). Other models relate to the stability of inlet systems.

Figure 5.21. Idealized ocean-inlet-bay system (adapted from USACE 1984)
Beaches adjacent to and near tidal inlets are part of the dynamic littoral system of the inlet and exhibit much more shoreline change than beaches farther from inlets. Sometimes the shoreline movement is erosion and sometimes it is accretion. The beaches near inlets can increase dramatically in width as some of the shoals migrate onshore. Inlet geometry can change dramatically in both the short-term and the long-term. A single storm can move hundreds of thousands of cubic yards of sand shoals into or out of an inlet. Some inlets have a tendency to migrate along the coast. Some migrate in the direction of net longshore sand transport and some migrate in the other direction.
There are a number of empirical relationships that have been recognized between the components of tidal inlet systems. Figure 5.22 shows one empirical relationship between tidal prism and inlet throat area. Tidal prism is defined as the amount of water that moves into and out of a tidal inlet during a tidal cycle. It is essentially the area of the bay multiplied by the bay tide range.
All tidal inlets are evolving and changing over the long-term. This evolution is in response to many changing factors including sea level rise, changes in longshore sand transport rate and changes in tidal prisms. These factors change naturally but also can be changed by engineering. Engineered changes to the ocean-inlet-bay system include the stabilization of the inlet with jetties or the dredging of the inlet or bay for navigation.

Figure 5.22. Tidal prism versus minimum inlet throat area for all major inlets on the Atlantic, Gulf, and Pacific coasts (USACE 1984)
Less obvious changes include the impact of engineering works in the bay that affect the tidal prism. This can be the filling of wetlands or the construction of causeways in the bay. The implication of the relationship shown in Figure 5.22 is that any change in the tidal prism of a bay can affect the inlet and, vice-versa, changes in the inlet; including shoaling, scour, dredging and engineered structures; can affect the tidal flow.
The two inlets shown in Figure 5.19 are evolving in response to a number of factors including the original creation of Lido Key by filling many decades ago and the construction of causeways not shown inside the bay. Another factor in the evolution of those two inlets is the complexities added to the tidal hydraulics by the interconnectedness of the multiple inlets to the bay. Multiple inlet systems can evolve as one inlet captures more of the tidal prism and expands while allowing others to close.
5.7 Physical Models in Coastal Engineering
Coastal engineering, like the broader field of hydraulic engineering, relies on three complementary techniques to deal with the complex fluid flows typical of many projects: field measurements and observations, laboratory measurements and observations, and mathematical calculations (Hughes 1993). Laboratory studies are generally termed physical models because they are miniature reproductions of a physical system. In parallel to the physical model is the numerical model, which is a mathematical representation of a physical system based on assumed governing equations and solved using a computer (Hughes 1993).
The use of physical models in coastal engineering has evolved in response to the development of numerical models. For example, in the mid-1900’s, large physical models of tidal estuary systems were used to understand the complex flows and analyze the influence of major engineering works. However, “large physical models of tidal estuary systems have now been almost totally replaced with numerical models that can predict flows with a good degree of success” (Hughes 1993).
There is still a critically important role for physical models in coastal engineering to address other types of problems (beyond the estuary tidal circulation problem). This is particularly true for understanding complex flows around structures where wave and current-induced turbulence issues reduce the usefulness of mathematical-numerical approaches. This is also true for newer fluid-structure-sediment-interaction problems that have not been tested extensively. Physical model tests are often performed to calibrate empirical coefficients in the numerical model or to validate the results of the numerical models. “Hybrid modeling” is the use of both physical and numerical models together to complement each technique (Hughes 1993).
There is a role for physical models in coastal engineering applications to highways for both reasons given above; the complex flows and the newer problems. For example, the problem of wave loads on bridge decks (Chapter 10) has recently been investigated with physical models in several different laboratories. Figure 5.23 shows an instrumented, 1:15 scale model of a bridge deck subjected to waves in one of those tests. The instrumented section is the middle section made of clear plexiglass. This problem of wave loads on bridge decks involves extremely complex flows. They have recently been the cause of significant damage to United States highways.
The use of physical models in coastal engineering is very much of an art as well as a science. Model to prototype similarity issues are extremely complex. There are a number of wave basins and flumes in universities and government laboratories that can conduct physical model tests. Hughes (1993) summarizes the issues and capabilities of physical models and laboratory techniques in coastal engineering.

Figure 5.23. Physical model test of wave loads on bridge decks (Texas A&M photo)
-
 SPW911 Sheet Pile Design Software
Rated 5.00 out of 5$150.00 – $599.99
SPW911 Sheet Pile Design Software
Rated 5.00 out of 5$150.00 – $599.99 -
 Sheet Pile Design (PDF Download)
Rated 5.00 out of 5$89.00
Sheet Pile Design (PDF Download)
Rated 5.00 out of 5$89.00 -
 Pile Driving (PDF Download)
$89.00
Pile Driving (PDF Download)
$89.00
-
 Marine Construction Volumes 1 & 2 (PDF Download)
$157.00
Marine Construction Volumes 1 & 2 (PDF Download)
$157.00
-
 Pile Driving (Book)
$89.00
Pile Driving (Book)
$89.00










